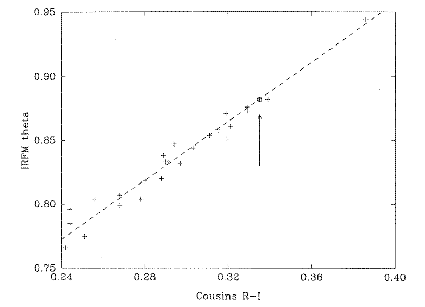
FIGURE 1.
Why search for stars which are identical solar twins? Note that

But if one were to use an ideal solar twin instead, one would
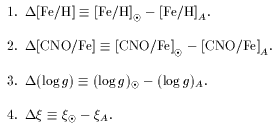
Using those differences, let a function
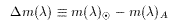
be obtained by differencing two synthetic spectra. This function has a resolution which is higher than any used in photometry or spectrophotometry, and it is published for general use in both kinds of observing.
To show how the function is to be applied, consider observers who are determining asteroid albedoes using filter photometry. Presumably those observers would compare their asteroid measurements to measurements of a real solar twin if such a thing were available. Instead, those observers now measure star A. Using results obtained by integrating Delta m(lambda) over their passbands, they then convert their measurements of star A to measurements of a fictitious star A' which is identical to the Sun. They then compare their asteroid data to their results for star A'.
To generalize this idea, let standard stars A, B, C, ... be chosen so that one of these stars is always available to an observer in either hemisphere. Let a function Delta m(lambda) be determined for each star. The observers may now recover measurements of fictitious solar twins A', B', C' ... The consistency of those measurements can then be used to find out how well the use of fictitious solar twins is working. If all goes as it should, the results for the fictitious solar twins will be consistent because the original stars were not too different from the Sun to begin with.
With these specifics in mind, a conjecture can be advanced (in the spirit of conjectures by mathematicians about unproved theorems):
By constructing fictitious solar twins in the ways described (and possibly other ways as well), one can make it unnecessary to search for real stars which are identical to the Sun.
I invite readers to talk to me about support or disproof (especially disproof) for this conjecture.